The equations of motion are
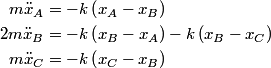 The normal mode frequencies are found by setting 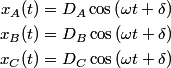 which gives 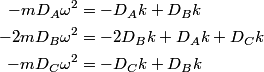 which can be written in matrix form 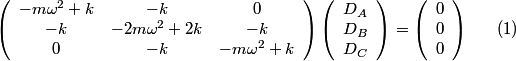 There is a non-trivial solution for 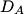 , , 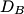 , and , and 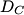 if and only if the matrix if and only if the matrix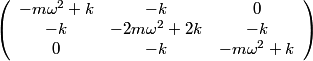 has zero determinant. Upon setting the determinant equal to 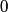 and solving the resulting equation for and solving the resulting equation for  , one will presumably find that , one will presumably find that 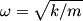 is a solution. Plug is a solution. Plug 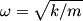 into equation (16) and solve for into equation (16) and solve for 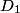 , , 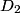 , and , and 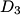 . This leads to . This leads to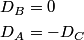 which means that the motion corresponding to this normal mode is given by 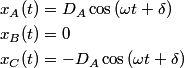 The statement that describes this motion is 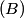 . Therefore, answer (B) is correct. . Therefore, answer (B) is correct. |